Олимпиадная задача по комбинаторной геометрии для 7–9 классов — раскраска доски 5×5

  Предположим, что существует раскраска таблицы 5×5, удовлетворяющая условию.

  В каждом столбце найдётся цвет, в который покрашены по крайней мере две клетки этого столбца. Назовём такой цвет преобладающим для данного столбца (возможно, у какого-то столбца будет два преобладающих цвета).

  Аналогично какой-то цвет (назовём его 1) будет преобладающим для двух столбцов. Поскольку от перестановки строк и столбцов ничего не зависит, будем считать, что это столбцы a и b. Также можно считать, что в первом столбце цветом 1 покрашены клетки a4 и a5. Тогда клетки b4 и b5 должны быть покрашены какими-то двумя различными цветами, отличными от цвета 1. Пусть они покрашены цветами 2 и 3, а поскольку цвет 1 – преобладающий для столбца b, можно считать, что клетки b2 и b3 покрашены цветом 1.

  Рассмотрим клетку a3. Выбрав 3-ю и 5-ю строки и столбцы a и b, мы получим, что клетка a3 не может быть покрашенной цветами 1 и 2. Аналогично она не может быть покрашенной цветами 1 и 2 и, следовательно, покрашена цветом 4. Из аналогичных рассуждений получаем, что и клетка a2 покрашена цветом 4.

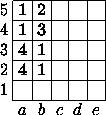
  Значит, квадрат, состоящий из клеток a3, a2, b3 и b2, покрашен в два цвета. Противоречие.

Нельзя.