Олимпиадная задача Лифшица Ю.: треугольники и три семейства параллельных прямых
Задача
Проведено три семейства параллельных прямых, по 10 прямых в каждом. Какое наибольшее число треугольников они могут вырезать из плоскости?
Решение
Рассмотрим 100 узлов – точек пересечения прямых первого и второго направлений. Разобьём их на 10 уголков: первый уголок – узлы, лежащие на первых прямых первого и второго направления. Второй – лежащие на вторых прямых (кроме точек, лежащих в первом уголке) и т. д. Треугольники со сторонами, параллельными трём фиксированным направлениям, могут иметь две ориентации, причём каждый из наших 100 узлов может быть вершиной не более одного треугольника каждой ориентации.
Поэтому 10 прямых третьего направления образуют не более 2·25 треугольников с последними пятью уголками, так как эти пять уголков содержат всего 25 узлов.
Заметим далее, что каждая из прямых третьего направления образует не более одного треугольника каждой ориентации с узлами, принадлежащими одному уголку. Поэтому треугольников, имеющих вершины в узлах остальных пяти уголков, будет не больше 10·2·5.
Итого треугольников не более 100 + 50 = 150.
Пример со 150 треугольниками приведён на рисунке.
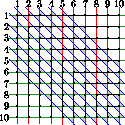
Ответ
150 треугольников.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь