Олимпиадная задача по стереометрии: максимум 6 больших граней многогранника, 10–11 класс
Задача
Многогранник описан около сферы. Назовем его грань большой, если проекция сферы на плоскость грани целиком попадает в грань. Докажите, что больших граней не больше 6.
Решение
Предположим, что утверждение задачи неверно и больших граней не менее 7.
Тогда мы получаем 7 векторов 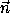 1,..,
1,..,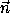 7 , углы между которыми не
меньше90o (для параллельных граней такой угол равен180o ).
7 , углы между которыми не
меньше90o (для параллельных граней такой угол равен180o ).
Отложим все векторы от одной точки P и проведем плоскость β ,
проходящую через P и не содержащую ни один из 7 векторов. Тогда по одну
сторону от нее будут отложены по крайней мере 4 вектора
(например, 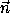 1,..,
1,..,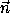 4 ). Разложим каждый из них в сумму двух:
4 ). Разложим каждый из них в сумму двух:
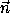 i=
i=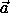 i+
i+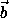 i , где
i , где 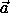 i
i β ,
β , 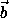 i
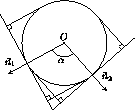
i β (см. рис. 2).
При этом можно считать, что
β (см. рис. 2).
При этом можно считать, что 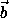 1=
1=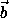 2=
2=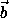 3=
3=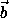 4=
4=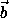 ,
где |
,
где |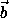 |=1.
По нашему предположению(
|=1.
По нашему предположению(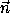 i,
i,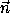 j)
j) 0, так как углы между
векторами не острые.
0, так как углы между
векторами не острые.
 i,
i,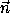 j)=(
j)=(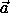 i+
i+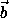 i,
i,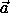 j+
j+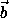 j)=
(
j)=
(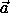 i,
i,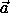 j)+1, так как(
j)+1, так как(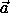 i,
i,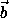 j)=(
j)=(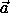 j,
j,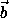 i)=0,(
i)=0,(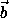 i,
i,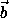 j)=
j)=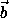 2=1.
Итак, для четырех векторов
2=1.
Итак, для четырех векторов 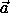 1,..,
1,..,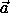 4 , лежащих в плоскости β ,(
4 , лежащих в плоскости β ,(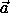 i,
i,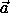 j)<0, что невозможно, так как угол хотя бы
между двумя из них не тупой. Противоречие, значит, наше предположение о
наличии у многогранника 7 больших граней неверно. 6 больших граней
есть у куба.
Второе решение. Пусть R – радиус шара. Сопоставим каждой большой грани часть граничной
сферы шара, расположенную в конусе, вершиной которого служит центр шара, а
основанием – проекция шара на эту грань. Указанная часть сферы является
сферической шапочкой (т.е. частью сферы, лежащей по одну сторону от
секущей сферу плоскости) высоты h=R(1-
j)<0, что невозможно, так как угол хотя бы
между двумя из них не тупой. Противоречие, значит, наше предположение о
наличии у многогранника 7 больших граней неверно. 6 больших граней
есть у куба.
Второе решение. Пусть R – радиус шара. Сопоставим каждой большой грани часть граничной
сферы шара, расположенную в конусе, вершиной которого служит центр шара, а
основанием – проекция шара на эту грань. Указанная часть сферы является
сферической шапочкой (т.е. частью сферы, лежащей по одну сторону от
секущей сферу плоскости) высоты h=R(1-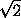 /2). По известной формуле
площадь такой шапочки равна2π Rh=π R2(2-
/2). По известной формуле
площадь такой шапочки равна2π Rh=π R2(2-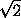 ). Так как
указанные шапочки не перекрываются, сумма их площадей не превосходит
площади сферы. Обозначив количество больших граней через n , получим n(2-
). Так как
указанные шапочки не перекрываются, сумма их площадей не превосходит
площади сферы. Обозначив количество больших граней через n , получим n(2-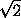 )
) 4, т.е. n
4, т.е. n
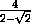 . Решение
заканчивается проверкой того, что
. Решение
заканчивается проверкой того, что 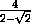 <7.
<7.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь