Олимпиадная задача по геометрии о циркуле на клетчатой бумаге (8–11 класс)

  Введём на листе прямоугольную систему координат с осями, параллельными линиям сетки, и началом координат в одном из узлов. Назовём чётностью узла чётность суммы его координат. Будем считать одну из ножек циркуля первой, а другую – второй и посмотрим, как меняется чётность узлов, в которые попадает вторая ножка при выполнении шагов. Обозначим вектор, соединяющий первую ножку со второй после i-го шага, через  (x_i, y_i),  i = 1, 2, ...,  тогда 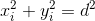   – квадрату раствора циркуля – целому числу. Рассмотрим три возможных случая.

  1)  d² – нечётно. Тогда во всех парах  (x_i, y_i)  одно из чисел чётно, другое нечётно, поэтому  x_i + y_i  нечётно, и на i-м шаге чётность основания передвигаемой ножки изменяется на  x_i + y_i – x_i–1 – y_i–1 = 2k_i,  то есть сохраняется. Чётность неподвижной ножки, очевидно, тоже сохраняется. Поскольку изначально чётности ножек были различны (в силу нечётности числа  d ≡ x₀ + y₀ (mod 2)),  поменяться местами ножки не смогут.

  2)  d² = 4n + 2.  Тогда все числа x_i, y_i нечётны, и координаты оснований ножек изменяются на i-м шаге на  x_i – x_i–1 = 2k_i  или  y_i – y_i–1 = 2l_i,  сохраняя свою чётность.

  И снова, поскольку изначально чётности разных ножек по каждой из координат были различны (в силу нечётности x₀ и y₀), ножки циркуля не смогут поменяться местами.

  в)  d² = 4n.  В этом случае все числа x_i, y_i чётны.

  Рассмотрим вместо исходной новую сетку, у которой ячейки – квадраты со стороной в два раза больше, причём ножки циркуля исходно располагаются в её узлах. Тогда шаги циркуля будут выполняться по узлам новой сетки, а для неё выполнен один из случаев 1), 2) или 3). При этом квадрат длины в новой сетке уменьшился в 4 раза (из-за выбора новой единицы измерения), поэтому случай 3) не может продолжаться до бесконечности.

Нельзя.