Олимпиадная задача по алгебре: уравнение с многочленами для 9-10 класса (Шаповалов А. В.)
Задача
Решите уравнение {(x + 1)³} = x³.
Решение
Из определения дробной части следует, что 0 ≤ x³ < 1, то есть 0 ≤ x < 1. Равенство {a + b} = a выполняется тогда и только тогда, когда b – целое число. Поэтому число n = 3x² + 3x – целое. Функция y = 3x³ + 3x возрастает на [0, 1], y(0) = 0, y(1) = 6, поэтому 0 ≤ n < 6, и из корней уравнения
3x² + 3x – n = 0 выбирается лежащий на промежутке [0, 1).
Ответ
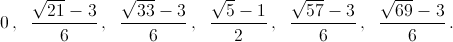
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет