Олимпиадная задача по планиметрии и комбинаторной геометрии для 9-11 классов
Задача
Докажите, что из любого конечного множества точек на плоскости можно так удалить одну точку, что оставшееся множество можно разбить на две части меньшего диаметра. (Диаметр – это максимальное расстояние между точками множества.)
Решение
Пусть A и B – любые две точки данного множества M ,
расстояние между которыми равно диаметру d этого множества.
Тогда из определения диаметра следует, что если P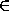
M ,
то P лежит внутри или на границе линзы, образованной
пересечением кругов радиуса d с центрами A и B (см. рис.) . Докажем, что на одной из дуг AKC и BLD нет точек множества M , т.е. что если K
A , L B , то KL>d .
Действительно, если 
BAK=α , LAK=β , то β>α ,
и из теоремы косинусов получаем
KL2=AK2+d2-2AKd cosβ>d2,
Пусть, например, на дуге AC нет точек множества M за исключением точки A . Тогда, выбросив точку A и разделив оставшееся множество точек на части по прямой AB , получим искомое разбиение, добавив точки прямой AB к левой части, так как в каждой половине линзы только расстояния от границ до точек A или B могут равняться d .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь