Олимпиадная задача Агханова: совпадение корней уравнений с параметрами, тригонометрия
Задача
Пусть f(x)=x2+ax+b cos x . Найдите все значения параметров a и b , при которых уравнения f(x)=0и f(f(x))=0имеют совпадающие непустые множества действительных корней.
Решение
Пусть x0 – общий корень, тогда f(x0)=0и f(f(x0))=0. Подставив первое равенство во второе,
получаем f(0)=0, т.е. b=0. Итак, f(x)=x2+ax ,
и уравнение f(x)=0имеет корни 0 и-a .
Далее, f(f(x))=0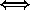
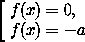
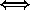
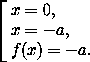Условие задачи выполнено, если каждый корень уравнения f(x)=-a равен 0 или-a .
Поэтому случаи a
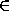(0,4), a=0подходят, так как уравнение f(x)=-a либо не имеет корней,
либо имеет корень 0. При остальных значениях a уравнение f(x)=-a имеет хотя бы один корень,
не совпадающий с 0 и-a .
Ответ
b=0,0
a<4.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет