Олимпиадная задача по математическому анализу для 9-11 классов от Сонкина М.
Задача
Докажите, что если
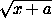 +
+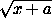 +
+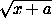 =
=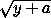 +
+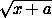 +
+ =
=
=
=
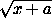 +
+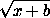 +
+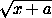
Решение
Без ограничения общности можем считать, что a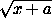 b
b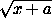 c .
Пусть не все числа x , y , z равны. Тогда среди них есть либо строго
наибольшее, либо строго наименьшее – скажем, x .
Заметим, что если β>α , то функция ϕ(t)=
c .
Пусть не все числа x , y , z равны. Тогда среди них есть либо строго
наибольшее, либо строго наименьшее – скажем, x .
Заметим, что если β>α , то функция ϕ(t)=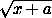 -
-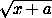 =
=
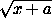 – монотонно
убывает.
– монотонно
убывает.
Перепишем первое из данных в условии равенств так:
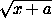 -
-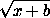 )+(
)+(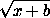 -
- )=
)=
=(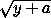 -
-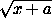 )+(
)+(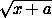 -
-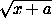 ).
).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет