Олимпиадная задача по математике: функция с параметром α, методы решения, 10-11 класс
Задача
Для каких α существует функция f :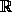 
,
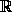
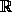отличная от константы, такая, что
f(α(x+y))=f(x)+f(y);?
Решение
Для α=1– существует: f(x)=x . Для α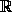
1для любого x существует y такое, что y=α(x+y): достаточно положить y=
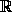. Но тогда из данного уравнения получаем f(y)=f(x)+f(y),
откуда f(x)=0для любого x .
Ответ
α=1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет