Олимпиадная задача по геометрии: Отражения внутри квадрата, Канель-Белов, 8–11 класс
Задача
Все вершины треугольника ABC лежат внутри квадрата K . Докажите, что если все их отразить симметрично относительно точки пересечения медиан треугольника ABC , то хотя бы одна из полученных трех точек окажется внутри K .
Решение
Пусть M(x0,y0)– точка пересечения медиан.
Прямая x=x0 делит квадрат на две части. В одной из частей
находится ровно одна вершина треугольника. Пусть ее
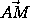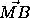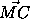координаты A(x1,y1), а координаты двух других B(x2,y2), C(x3,y3). Тогда 
=
+
и, значит, |x0-x1|=|x0-x2|+|x0-x3| . Поэтому после отражения
относительно точки M точки B и C перейдут в полосу,
ограниченную прямыми x=x0 и x=x1 .
Проведя аналогичные рассуждения для y , получим, что какие-то две
точки перешли в полосу, ограниченную прямыми y=y0 и y=y (где y – ордината одной из вершин треугольника).
Одна из этих точек будет B или C , после отражения относительно M она, как мы доказали, останется внутри квадрата.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь