Олимпиадная задача: точечный прожектор и треугольник, планиметрия, 7–9 класс
Задача
Точечный прожектор, находящийся в вершине B равностороннего треугольника ABC, освещает угол α. Найдите все такие значения α, не превосходящие 60°, что при любом положении прожектора, когда освещенный угол целиком находится внутри угла ABC, из освещенного и двух неосвещенных отрезков стороны AC можно составить треугольник.
Решение
Пусть α < 30°. Расположим прожектор так, чтобы один из крайних лучей BK был перпендикулярен AC (рис. слева). Второй луч пересекает основание в точке M. Но AK = KC = KM + MC. Значит, из этих отрезков сложить треугольник нельзя.
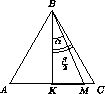
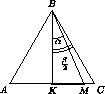
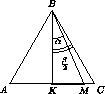
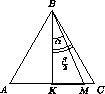
Ответ
α = 30°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет