Олимпиадная задача по математике: значения числового выражения при взаимно простых a, b и c
Задача
Пусть a, b и c – попарно взаимно простые натуральные числа. Найдите все возможные значения 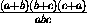 , если известно, что это число целое.
, если известно, что это число целое.
Решение
Пусть (a + b)(b + c)(c + a) = nabc, где n – целое число.
Пусть среди чисел a, b и c есть равные, например, a = b. Тогда (a, b) = a = 1 и 2(1 + c)2 = nc. Отсюда следует, что 2 делится на c, то есть c = 1 или 2. В первом случае n = 8, а во втором n = 9.
Пусть a < b < c. Если два числа взаимно просты, то сумма этих чисел взаимно проста с каждым из них, поэтому a + b = mc, a + c = kb (m и k – натуральные).
Так как a + b < 2c, то mc < 2c и, значит, m < 2, то есть m = 1 и, следовательно, a + b = c. Значит, a + b = kb – a, или 2a = b(k – 1).
Так как a и b взаимно просты, то 2 делится на b. Учитывая, что 1 ≤ a < b, получаем, что b > 1 и, значит, b = 2. Тогда a = 1, c = 3, n = 10.
Ответ
8, 9, 10.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь