Олимпиадная задача по комбинаторной геометрии для 8–11 классов с Петей и Васей

Докажем, что Вася достигнет максимума, если поступит следующим образом: в первой паре – первая слева красная точка и первая справа синяя, во второй паре – вторая слева красная и вторая справа синяя, и т.д.

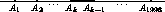
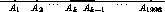Для этого соединим точки в каждой паре отрезком и сосчитаем, сколько из этих отрезков покрывают отрезок A_k A_{k +} 1 (см. рис.) . Пусть k 998, и среди точек A1, A_k l красных. Тогда справа от точки A_k не менее l синих точек (если меньше, то среди A1, A_k больше, чем998 - l синих, и k > 998). Следовательно, все отрезки, красные концы которых находятся среди точек A1, A_k , покрывают отрезок A_k A_{k +} 1. То же верно с заменой красных концов на синие. То есть отрезок A_k A_{k +} 1покрыт k отрезками, а большим числом он и не может быть покрыт. Аналогично, при k>998отрезок A_kA_k+1покрыт1996-k отрезками, и не может быть покрыт большим числом отрезков. Следовательно, сумма, достигнутая Васей, равна1 + 2 +...+ 997 + 998 + 997 +...+ 2 + 1 = 9982и не зависит от раскраски.

Ответ задачи отсутствует