Олимпиадная задача по теории чисел и последовательностям от Канеля-Белова для 9-11 классов
Задача
Существует ли такая бесконечная периодическая последовательность, состоящая из букв a и b, что при одновременной замене всех букв a на aba и букв b на bba она переходит в себя (возможно, со сдвигом)?
Решение
Натуральное число n назовём периодом периодической последовательности x1x2..., если xi = xi+n для всех i = 1, 2, ... . Легко доказать, что
любой период кратен наименьшему;
для любого k наименьшие периоды последовательностей x1x2... и xk+1xk+2... совпадают.
Пусть x1x2... – последовательность, удовлетворяющая условиям задачи, и n – её наименьший период. Рассмотрим три случая.
1) n = 3m. Число m не является периодом последовательности (m < n), поэтому найдётся такая пара xi, xi+m, что xi ≠ xi+m. Заменив все буквы xi, ..., xi+m по правилу a → aba, b → bba, мы получим фрагмент последовательности: 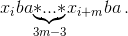 (1)
(1)
Но, согласно сделанным замечаниям, из того, что n = 3m, следует, что начальная тройка букв этого фрагмента совпадает с конечной. Противоречие.
2) n = 3m + 1. Тогда, как и выше, найдётся пара xi ≠ xi+m. Но тогда вторая буква фрагмента (1) должна совпадать с последней, что не так.
3) n = 3m – 1. Тогда третья буква фрагмента (1) должна совпадать с предпоследней. Противоречие.
Ответ
Не существует.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь