Назад

Олимпиадная задача по планиметрии и комбинаторной геометрии для 8-10 классов: правильный шестиугольник, отмеченные узлы и окружность

Задача 209877 • Сложность: 2 • 8-10 класс
Задача

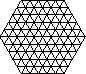
Правильный шестиугольник со стороной 5 разбит прямыми, параллельными его сторонам, на правильные треугольники со стороной 1 (см. рис.).

Назовём узлами вершины всех таких треугольников. Известно, что более половины узлов отмечено. Докажите, что найдутся пять отмеченных узлов, лежащих на одной окружности.
Авторы:
Кузнецов Д. Ю.
Разделы:
Планиметрия Комбинаторная геометрия Принцип Дирихле
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 1994-1995 Региональный этап
Количество версий:
5
Решение

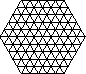
Общее количество узлов равно  2·(6 + 7 + 8 + 9 + 10) = 91.  Каждый узел, за исключением центрального, принадлежит одной из 11 концентрических окружностей с центром в центре шестиугольника (см. рис.).

Предположим, что не существует пяти отмеченных узлов, лежащих на одной окружности. Тогда общее количество отмеченных узлов не больше 11·4 + 1 = 45,  то есть не более половины. Противоречие.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет