Олимпиадная задача по планиметрии для 9–11 классов от Токарева С. И.: Раскраска сторон и диагоналей 12-угольника
Задача
Все стороны и диагонали правильного 12-угольника раскрашиваются в 12 цветов (каждый отрезок – одним цветом).
Существует ли такая раскраска, что для любых трёх цветов найдутся три вершины, попарно соединенные между собой отрезками этих цветов?
Решение
Допустим, такая раскраска возможна. Первый способ. Рассмотрим отрезки какого-либо одного цвета, например, красного. Общее число треугольников, одна из сторон которого красная, не меньше числа пар из 11 остальных цветов, то есть 55. Так как каждый красный отрезок служит стороной для десяти треугольников, то число красных отрезков не меньше шести. Но тогда и число отрезков любого другого цвета не меньше шести, а общее число отрезков не меньше 12·6 = 72. Однако число всех сторон и диагоналей в 12-угольнике равно 12·11 : 2 = 66 < 72. Противоречие. Второй способ. Поскольку число всех возможных треугольников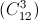 
равно числу троек цветов, то каждый треугольник раскрашен "правильно" и каждый "вид" раскраски реализуется ровно один раз. Поэтому треугольников с красной стороной ровно 55. Но каждый красный отрезок служит стороной десяти треугольников, а 55 на 10 не делится. Противоречие.
Ответ
Не существует.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь