Назад

Олимпиадная задача по тригонометрии и геометрии 10–11 класс Галочкин А. И.

Задача 209860 • Сложность: 4 • 10-11 класс
Задача

Для углов α , β , γ справедливо равенство sinα + sinβ + sinγ 2. Докажите, что cosα + cosβ + cosγ .

Авторы:
Галочкин А. И.
Разделы:
Тригонометрия Планиметрия Геометрические методы
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 1994-1995 Региональный этап
Количество версий:
4
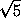Решение

Предположим противное: cosα + cosβ + cosγ >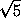 . Тогда для векторов 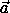=( sinα , cosα ), 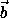=( sinβ , cosβ )и 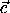=( sinγ , cosγ )имеем:3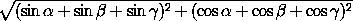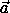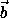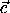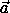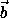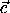<= |++|||+||+||=3. Получили противоречие.

Сумму

A=( sinα + sinβ + sinγ )2+( cosα + cosβ + cosγ)2

легко оценить сверху:

A=( sin2α + cos2α )+( sin2β + cos2β ) +( sin2γ + cos2γ )+ + 2( sinα sinβ + cosα cosβ) +2( sinα sinγ + cosα cosγ )+ + 2( sinβ sinγ + cosβ cosγ ) 3+3· 2=9.

Отсюда

( cosα + cosβ + cosγ)2 =A-( sinα + sinβ + sinγ)2 9-4=5.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет