Олимпиадная задача Богданова: равенство сумм и корней для натуральных чисел (9–11 класс)
Задача
Существуют ли такие попарно различные натуральные числа m, n, p, q, что m + n = p + q и 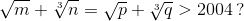
Решение
Будем искать такие числа в виде m = a², n = b³, p = c², q = d³, где a, b, c, d – натуральные. Тогда a + b = c + d, a² + b³ = c² + d³, то есть a – c = d – b,
(a – c)(a + c) = (d – b)(d² + bd + b²). Зафиксируем такие b и d, что b = d – 1 > 2004. Тогда условиям удовлетворяет пара c = ½ (d² + bd + b² – 1),
a = ½ (d² + bd + b² + 1); эти числа целые, поскольку b и d разной чётности. Кроме того, a > c > b² > d > b > 2004.
Ответ
Существуют.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет