Олимпиадная задача по планиметрии и комбинаторной геометрии для 8–10 классов: центральная симметрия треугольника внутри выпуклого многоугольника
Задача
Треугольник T содержится внутри выпуклого центрально-симметричного многоугольника M . Треугольник T' получается из треугольника T центральной симметрией относительно некоторой точки P , лежащей внутри треугольника T . Докажите, что хотя бы одна из вершин треугольника T' лежит внутри или на границе многоугольника M .
Решение
Второе решение. Докажем простуюлемму:если на плоскости дан треугольник XYZ и точка S , то треугольник XYZ покрывается треугольниками SXY , SYZ , SZX .
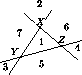
Действительно, прямые XY , YZ , ZX разбивают плоскость на 7 частей (см. рис. 2) .
Если S лежит в части 1, то Δ XYZ = Δ SXY 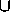 Δ SYZ
Δ SYZ 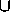 Δ SZX ; если S лежит в части 2,
то Δ XYZ
Δ SZX ; если S лежит в части 2,
то Δ XYZ 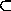 Δ SYZ (рассмотрения для частей 3, 4 аналогичны);
если S лежит в части 5, то Δ XYZ
Δ SYZ (рассмотрения для частей 3, 4 аналогичны);
если S лежит в части 5, то Δ XYZ 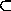 Δ SXY
Δ SXY 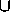 Δ SZX (рассмотрения для частей 6, 7 аналогичны).
Δ SZX (рассмотрения для частей 6, 7 аналогичны).
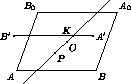
Перейдем к решению задачи. Обозначим через O центр симметрии многоугольника M , через A , B , C – вершины треугольника T , а через A1 , B1 , C1 – середины сторон BC , CA , AB соответственно.
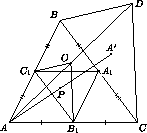
Определим также VB и VC как выпуклые оболочки четверок O , B , C1 , A1 и O , C , A1 , B1 .
При этом VB покрывает Δ B A1 C1 , VC покрывает Δ C A1B1 .
Кроме того, VA  Δ O B1 C1 , VB
Δ O B1 C1 , VB  Δ O C1 A1 , VC
Δ O C1 A1 , VC  Δ O A1 B1.
Отсюда, применяялемму, получаем, что
объединение V многоугольников VA , VB , VC покрывает Δ A1 B1C1 .
Итак, V покрывает объединение треугольников A B1 C1 , B A1 C1 , C A1 B1 , A1 B1 C1 , т.е. V покрывает Δ A B C . Это означает, что один из
многоугольников VA , VB , VC содержит точку P ,
пусть, для определенности, P
Δ O A1 B1.
Отсюда, применяялемму, получаем, что
объединение V многоугольников VA , VB , VC покрывает Δ A1 B1C1 .
Итак, V покрывает объединение треугольников A B1 C1 , B A1 C1 , C A1 B1 , A1 B1 C1 , т.е. V покрывает Δ A B C . Это означает, что один из
многоугольников VA , VB , VC содержит точку P ,
пусть, для определенности, P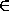 VA (см. рис. 3).
VA (см. рис. 3).
Пусть A' – вершина треугольника T' , т.е. точка, симметричная точке A относительно P ; пусть D – точка, симметричная точке A относительно O . При гомотетии с центром в точке A и коэффициентом k=2точка P перейдет в A' , O перейдет в D , C1 перейдет в B , B1 перейдет в C . Следовательно, многоугольник VA перейдет в выпуклую оболочку U точек D , A , C , B , причем точка A' содержится в U .
Так как A, B, C 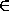 M и M симметричен относительно O , то D
M и M симметричен относительно O , то D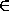 M . Поскольку M – выпуклый, U
M . Поскольку M – выпуклый, U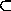 M .
Значит, A'
M .
Значит, A'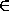 M , что и требовалось.
M , что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь