Олимпиадная задача по стереометрии для 10–11 класса: секущие шестиугольники в параллелепипеде
Задача
В прямоугольном параллелепипеде проведено сечение, являющееся шестиугольником. Известно, что этот шестиугольник можно поместить в некоторый прямоугольник Π . Докажите, что в прямоугольник Π можно поместить одну из граней параллелепипеда.
Решение
Пусть ABCDA1B1C1D1 – прямоугольный параллелепипед, в
котором AB=a , AD=b , AA1=c , причем a  b
b  c .
c .
Без ограничения общности можно считать, что шестиугольное сечение KLMNPQ расположено так, что K AD , L
AD , L AB , M
AB , M BB1 , N
BB1 , N B1C1 , P
B1C1 , P  C1D1 , Q
C1D1 , Q  D1D (см. рис. 1) .
D1D (см. рис. 1) .

Рис. 1
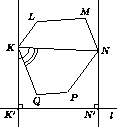
Рис. 2
Докажем, что проекция шестиугольника KLMNPQ на любую прямую, лежащую в плоскости этого шестиугольника, не меньше, чем a .
Поскольку противоположные стороны шестиугольника KLMNPQ параллельны, его проекция на некоторую прямую l будет совпадать с проекцией одного из отрезков KN , LP , MQ . Пусть, для определенности, проекция на l совпадает с отрезком K'N' , где K' и N' – проекции точек K и N соответственно. Можно предполагать, что K' , N' , P и Q лежат по одну сторону от KN (этого можно добиться параллельным сдвигом l ).
Тогда один из углов K'KN , N'NK – не тупой, пусть, например,  K'KN не тупой (см. рис. 2) . Тогда K'N' = KN sin
K'KN не тупой (см. рис. 2) . Тогда K'N' = KN sin K'KN
K'KN  KN sin
KN sin QKN .
Но KN sin
QKN .
Но KN sin QKN – это расстояние между прямыми QK и MN ,
поэтому K'N'
QKN – это расстояние между прямыми QK и MN ,
поэтому K'N'  KN sin
KN sin QKN
QKN  a .
a .
Пусть шестиугольник KLMNPQ помещен в прямоугольник Π со сторонами, равными d1 , d2 . Тогда каждая из сторон d1 , d2 не меньше, чем длина проекции KLMNPQ на прямые, параллельные сторонам Π . Отсюда по доказанному
d1  a, d2
a, d2  a.
(1)
a.
(1)
 AD1 =
AD1 =  .
С другой стороны, LP содержится в Π , поэтому
длина LP не превосходит длины диагонали
.
С другой стороны, LP содержится в Π , поэтому
длина LP не превосходит длины диагонали  прямоугольника Π .
Получаем, что
прямоугольника Π .
Получаем, что
d12+d22  b2+c2.
(2)
b2+c2.
(2)
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь