Олимпиадная задача по планиметрии и комбинаторной геометрии для 9–11 класса
Задача
Докажите, что не существует конечного множества, содержащего более2N ( N>3) попарно неколлинеарных векторов на плоскости, обладающего следующими двумя свойствами.
- Для любых N векторов этого множества найдется еще такой N-1 вектор из этого множества, что сумма всех 2N-1 векторов равна нулю;
- для любых N векторов этого множества найдутся еще такие N векторов из этого множества, что сумма всех 2N векторов равна нулю.
Решение
Предположим противное.
Выберем прямую, не ортогональную ни одному из векторов нашего
множества.
Тогда проекции хотя бы N векторов на нее направлены в одну
сторону; обозначим их 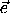 1 ,
1 , 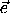 N.
N.
Введем на этой прямой
направление так, что эти векторы направлены в отрицательную сторону,
и выберем N векторов 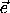 1 ,
1 , 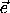 N так,
что алгебраическая проекция s их суммы максимальна (ясно, что из условия 2) s>0).
N так,
что алгебраическая проекция s их суммы максимальна (ясно, что из условия 2) s>0).
При этом, если некоторые из этих векторов совпали с векторами 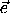 i , то проекции всех векторов,
кроме
i , то проекции всех векторов,
кроме 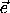 1 ,
1 , 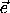 N , направлены в отрицательную сторону;
тогда мы обозначим через
N , направлены в отрицательную сторону;
тогда мы обозначим через 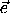 i какие-то N векторов, отличных от
i какие-то N векторов, отличных от 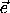 i , i=1, N .
i , i=1, N .
Для N векторов 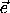 i найдутся векторы
i найдутся векторы 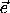 1 ,
1 , 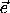 N-1такие, что
N-1такие, что 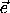 1+...+
1+...+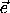 N=-(
N=-(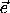 1+...+
1+...+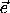 N-1). Хотя бы один из векторов
N-1). Хотя бы один из векторов 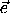 i не
совпадает ни с одним из
i не
совпадает ни с одним из 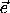 j (пусть это
j (пусть это 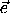 1 ), при этом
алгебраическая проекция суммы
1 ), при этом
алгебраическая проекция суммы 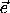 1+...+
1+...+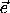 N-1+
N-1+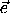 1 отрицательна и больше s по модулю.
Тогда для векторов
1 отрицательна и больше s по модулю.
Тогда для векторов 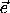 1 ,
1 , 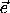 N-1,
N-1, 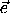 1 существуют N векторов, сумма которых равна-(
1 существуют N векторов, сумма которых равна-(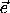 1+...+
1+...+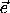 N-1+
N-1+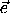 1), т.е.
алгебраическая проекция суммы которых больше s .
Противоречие с выбором векторов
1), т.е.
алгебраическая проекция суммы которых больше s .
Противоречие с выбором векторов 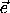 i .
i .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь