Олимпиадная задача по планиметрии для 9-11 классов с ортоцентрами и окружностями

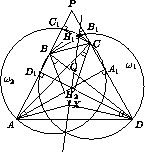
  Рассмотрим окружности ω₁ и ω₂, построенные на диагоналях AC и BD как на диаметрах. Пусть BB₁, CC₁, AA₁, DD₁ – высоты треугольников BPC и APD, соответственно (точки A₁ и C₁ лежат на ω₂, B₁ и D₁ – на ω₁). Тогда точки A, D₁, A₁, D лежат на одной окружности, поэтому  H₁A·H₁A₁ = H₁D·H₁D₁,  то есть H₁ лежит на радикальной оси ω₁ и ω₂. Аналогично H₂ также на ней лежит, следовательно, эта радикальная ось есть прямая H₁H₂.

  Обозначим черезMиNсередины диагоналейACиBDсоответственно.   Так как точкаXпо условию лежит на радикальной оси ω₁и ω₂, то  XM² –CM² =XN² –DN².  Но треугольникиXACиXBDподобны, так как ∠XAQ= ∠XBQ,  ∠XCQ= ∠XDQ,  следовательно, эти разности квадратов должны относиться как квадрат коэффициента подобия или равняться нулю.   Во втором случае  ∠AXC= ∠BXD= 90°,  но тогда прямыеABиCDперпендикулярны (так как одна из них получается из другой поворотной гомотетией с углом 90° и центромX), что противоречит различности точекH₁иH₂. Значит, треугольникиAXCиBXDравны. Но тогда равны и треугольникиAYCиDYB, так как они подобны (по причинам, аналогичным подобию треугольниковAXCиBXD) и имеют равные соответственные стороны  (AC = BD).   Значит, степени точкиYотносительно окружностей ω₁и ω₂равны (так как  YM = YN,  MC = ND),  поэтому она лежит на той же радикальной оси.

Ответ задачи отсутствует