Олимпиадная задача по принципу Дирихле: наибольшее N в таблице 20×20 (8-10 класс)
Задача
Найдите наибольшее натуральное число N, для которого при произвольной расстановке различных натуральных чисел от 1 до 400 в клетках квадратной таблицы 20×20 найдутся два числа, стоящих в одной строке или одном столбце, разность которых будет не меньше N.
Решение
Пример. Разделим таблицу на два прямоугольника 20×10 по вертикали. В первом прямоугольнике расставим числа от 1 до 200 по строкам в возрастающем порядке (в первой строке – от 1 до 10, во второй – от 11 до 20 и т.д.). Во втором расставим так же числа от 201 до 400. Тогда максимальная разность между числами в каждой строке равна 210 – 1 = 209, а в каждом столбце 191 – 190. Поэтому N ≤ 209.
Отметим все строки и столбцы, в которых есть числа от 1 до 91, красным, а все строки и столбцы, где есть числа от 300 до 400, второго – синим.
Пусть красным отмечено i строк и j столбцов. Тогда все числа от 1 до 91 находятся в клетках их пересечения, поэтому ij ≥ 91. Отсюда
i + j ≥ 2 
≥ 2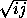 
> 19. Итак, красным отмечено не менее 20 линий (строк или столбцов).
Аналогично для k синих строк и l синих столбцов сумма k + l ≥ 2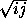 
> 20, то есть синим отмечено не менее 21 линии.
Отсюда следует, что какая-то линия будет отмечена и красным, и синим, и в ней максимальная разность чисел будет не меньше чем 300 – 91 = 209.
Ответ
N = 209.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь