Олимпиадная задача по планиметрии и комбинаторной геометрии 10-11 класса от Дольникова и Карасева
Задача
На плоскости дано конечное множество точек X и правильный треугольник T . Известно, что любое подмножество X' множества X , состоящее из не более9точек, можно покрыть двумя параллельными переносами треугольника T . Докажите, что все множество X можно покрыть двумя параллельными переносами T .
Решение
Нам понадобятся две леммы:
Лемма 1.Если два треугольника T1 и T2 гомотетичны с положительным коэффициентом и треугольник T2 пересекает каждую прямую, содержащую сторону треугольника T1 , то T2 содержит T1 . Доказательство.Очевидно.
Лемма 2.Для любого конечного множества точек M и треугольника T найдется треугольник T' , гомотетичный T с положительным коэффициентом, содержащий M и содержащий на каждой своей стороне какую-то точку из M . Доказательство.Рассмотрим какой-то треугольник, положительно гомотетичный T и содержащий M . Если какая-то его сторона не пересекается с M , уменьшим его гомотетией с центром в противоположной этой стороне вершине и добьемся, чтобы сторона пересеклась с M и треугольник все еще содержал M . Повторяя это для каждой стороны, получим требуемое.
Заметим, что в условии предыдущей леммы любой положительно гомотетичный T треугольник, содержащий M , содержит также и T' по лемме 1.
Теперь перейдем к решению задачи. Применимлемму 2к T и X . Получим треугольник, обозначим его для определенности ABC . На сторонах BC , AC и AB есть соответственно три точки xA , xB и xC из множества X , среди которых могут быть совпадающие.
Если ABC не превосходит T по размерам, доказательство очевидно закончено. Иначе рассмотрим три треугольника ABACA , ABBCB и ACBCC , положительно гомотетичные ABC с центрами в его вершинах и равные исходному T . Обозначим подмножества множества X
XA = X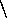 Δ ABACA
XB = X
Δ ABACA
XB = X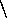 Δ ABBCB
XC = X
Δ ABBCB
XC = X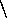 Δ ACBCC.
Δ ACBCC.
Лемма 3.Если какой-то треугольник T' , получающийся из T параллельным переносом, содержит точки xA и xB , то он не может пересекать множество XC . Аналогично для других пар точек и соответствующего им множества. Доказательство.Предположим противное. Так как T' содержит xA и xB , то одна из этих точек лежит по одну сторону с C относительно ACBC , иначе длина стороны T' больше ACBC .
Тогда можно заметить, что T' пересекает все прямые сторон ACBCC , а значит содержит ACBCC . Так как эти треугольники равны, то они совпадают, но тогда T' не может пересекать XCЛемма доказана.
Теперь применимлемму 2к треугольнику T и множествам XA , XB , XC , получим треугольники TA , TB , TC , причем на их сторонах можно выбрать точки {xAB, xAC, xA} , {xBA, xBC, xB} , {xCA, xCB, xC} соответственно (некоторые из них могут совпасть), лежащие в соответствующих множествах XA, XB, XC.
К точкам xA , xB , xC , xAB , xAC , xBA , xBC , xCA , xCB применим условие задачи. Они содержатся в треугольниках T1 и T2 , являющихся параллельными переносами T .
Какие-то две из первых трех точек содержатся в одном из этих треугольников, без
ограничения общности xA,xB 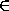 T1 . Тогда полемме 3треугольник T1 не
пересекает множество XC и все три точки xC , xCA , xCB содержатся в другом треугольнике T2 . Отсюда следует, что
множество XC содержится в T2 по лемме 1; значит, треугольники ACBCC и T2 покрывают все множество X .
T1 . Тогда полемме 3треугольник T1 не
пересекает множество XC и все три точки xC , xCA , xCB содержатся в другом треугольнике T2 . Отсюда следует, что
множество XC содержится в T2 по лемме 1; значит, треугольники ACBCC и T2 покрывают все множество X .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь