Олимпиадная задача: Рациональные выражения в числовом множестве, 9-11 класс
Задача
Числовое множество M , содержащее 2003 различных положительных числа, таково,
что для любых трех различных элементов a,b,c из M число a2+bc рационально.
Докажите, что можно выбрать такое натуральное n , что для любого a из M число a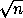 рационально.
рационально.
Решение
Возьмем четыре различных числа a,b,c,d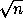 M .
Из рациональности чисел d2+ab и d2+bc следует рациональность bc-ab , откуда a2+ab=a2+bc-(bc-ab)
M .
Из рациональности чисел d2+ab и d2+bc следует рациональность bc-ab , откуда a2+ab=a2+bc-(bc-ab)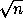
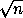 .
Аналогично, b2+ab
.
Аналогично, b2+ab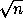
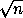 . Поэтому для произвольных различных a,b
. Поэтому для произвольных различных a,b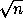 M число q=
M число q=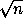 =
=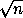
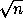
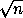 .
Тогда a=qb
.
Тогда a=qb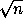 a2+ab=b2(q2+q)=l
a2+ab=b2(q2+q)=l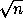
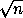 , b=
, b=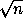 =
=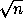 , m,k
, m,k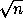
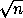 .
Значит, число b
.
Значит, число b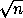 , где n=mk , рационально.
Тогда c
, где n=mk , рационально.
Тогда c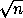 =
=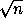 ·
b
·
b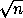
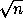
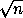 для любого c
для любого c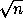 M .
M .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет