Назад

Олимпиадная задача по стереометрии для 10–11 класса: тетраэдр и вписанная сфера

Задача 209779 • Сложность: 1 • 10-11 класс
Задача

Вписанная в тетраэдр ABCD сфера касается его граней ABC , ABD , ACD и BCD в точках D1 , C1 , B1 и A1 соответственно. Рассмотрим плоскость, равноудаленную от точки A и плоскости B1C1D1 и три другие аналогично построенные плоскости. Докажите, что тетраэдр, образованный этими четырьмя плоскостями, имеет тот же центр описанной сферы, что и тетраэдр ABCD .

Авторы:
Бахарев Ф.
Разделы:
Стереометрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2002-2003 Заключительный этап
Количество версий:
4
Решение
Первое решение. Обозначим вершины получающегося тетраэдра A2 , B2 , C2 и D2 . Тогда тетраэдры A1B1C1D1 и A2B2C2D2 гомотетичны, причем эта гомотетия переводит центр вписанной сферы тетраэдра ABCD в центр описанной сферы тетраэдра A2B2C2D2 . Покажем, что она переводит центр вписанной сферы тетраэдра ABCD в центр описанной сферы тетраэдра ABCD .

Заметим, что точка A2 – радикальный центр трех точек: B , C , D и вписанной в тетраэдр ABCD сферы, поскольку является точкой пересечения трех радикальных плоскостей (именно эти плоскости рассматриваются в задаче). В связи с этим точка A2 равноудалена от вершин B , C и D . Поэтому прямая, проходящая через A2 перпендикулярно плоскости BCD , проходит через центр описанной сферы ABCD . Именно эта прямая является образом при гомотетии прямой, проходящей через A1 перпендикулярно BCD . Точка пересечения таких прямых – центр вписанной сферы ABCD – переходит таким образом в центр описанной сферы ABCD . Что и требовалось. Второе решение. Пусть O , OA , OB , OC , OD – центры описанных сфер тетраэдров ABCD , BCDI , ACDI , ABDI , ABCI соответственно ( I – центр вписанной в ABCD сферы). Покажем, что O – центр описанной сферы тетраэдра OAOBOCOD .

Действительно, отрезки OOA , OOB , OAOB перпендикулярны плоскостям BCD , ACD , ICD соответственно, причем плоскость ICD составляет равные углы с плоскостями BCD и ACD ; поэтому Δ OOAOB равнобедренный, OOA=OOB . Остальные равенства получаются аналогично. Тогда тетраэдры A1B1C1D1 и OAOBOCOD гомотетичны.

Отложим от точки OA вектор 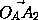=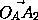/2, аналогично получаются точки B2 , C2 , D2 . Тогда, поскольку плоскости A1B1C1 и OAOBOC параллельны, то плоскость A2B2C2 также им параллельна; кроме того, поскольку OAOBOC – серединный перпендикуляр к DI , а расстояние между A2B2C2 и OAOBOC вдвое меньше расстояния между I и A1B1C1 , то A2B2C2 – плоскость, данная в условии. Но тогда из равенства OA2=OOA+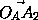 и аналогичных равенств следует требуемое.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет