Олимпиадная задача по планиметрии и многочленам: длины высот и стороны треугольника

Можно считать, что в данном уравнении  f(x) = 0  многочлен  f(x) приведённый. Из теоремы Виета следует, что если a, b, c – длины сторон треугольника, то числа  2p = a + b + c = A,  ab + bc + ba = B,  abc = C  рациональны. По формуле Герона  S² =  pf(p},  то есть S² тоже рационально. Из равенств  h_a = ^2S/_a,  h_b = ^2S/_b,  h_c = ^2S/_c  следует, что h_a, h_b, h_c – корни уравнения 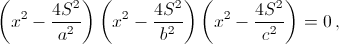    имеющего рациональные коэффициенты в силу тождеств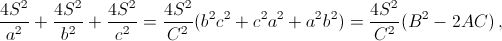      

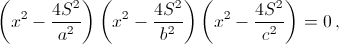
Ответ задачи отсутствует