Олимпиадная задача по тригонометрии для 10-11 класса: уравнение с синусами по Агханову, Голованову и Сендерову
Задача
Пусть α , β , γ , τ – такие положительные числа, что при всех x
sinα x+ sinβ x= sinγ x+ sinτ x.
Решение
Первое решение. Без ограничения общности можно считать α-β 0, γ-τ
0, γ-τ 0.
Положим a=
0.
Положим a=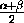 , b=
, b= , c=
, c=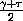 , d=
, d= , тогда условие задачи
перепишется в виде
, тогда условие задачи
перепишется в виде
где a>b 0, c>d
0, c>d 0.
0.
2 sin dx cos bx= sin cx.
Приравнивая наименьшие положительные корни левой и правой частей, получаем c=d (что невозможно) либо c=2b .
В последнем случае sin bx= sin dx , так что b=d .
Тогда sin ax= sin cx , т.е. a=c .
Так же a=c и b=d в случае  =
= .
Наконец, в случае
.
Наконец, в случае  =
= также получаем b=d и a=c .
также получаем b=d и a=c .
Продифференцируем данное равенство и положим x=0:
Возьмем третью производную и подставим x=0:
Мы получили систему
 αβ=γτ, α+β=γ+τ
αβ=γτ, α+β=γ+τ пары(α,β)и(γ,τ)совпадают, что и требовалось.
пары(α,β)и(γ,τ)совпадают, что и требовалось.
 0, γ-τ
0, γ-τ 0.
Положим a=
0.
Положим a=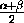 , b=
, b= , c=
, c=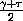 , d=
, d= , тогда условие задачи
перепишется в виде
, тогда условие задачи
перепишется в виде
sin ax cos bx= sin cx cos dx,
 0, c>d
0, c>d 0.
0.
Наименьший положительный корень x0 левой части– число  или
или  , а правой–
, а правой–  или
или  .
Если a=c , то cos bx= cos dx и, значит, b=d .
Из этих равенств следует требуемое.
.
Если a=c , то cos bx= cos dx и, значит, b=d .
Из этих равенств следует требуемое.
Пусть x0= . Если
. Если  =
= , то a=2d ,
и из равенства функций sin2dx cos bx= sin cx cos dx следует
, то a=2d ,
и из равенства функций sin2dx cos bx= sin cx cos dx следует
 =
= .
Наконец, в случае
.
Наконец, в случае  =
= также получаем b=d и a=c .
также получаем b=d и a=c .
Второе решение.
sinα x+ sinβ x= sinγ x+ sinτ x (1)
α cosα x+β cosβ x=γ cosγ x+τ cosτ x α+β=γ+τ.
α+β=γ+τ.
-α3 cosα x-β3 cosβ x=-γ3 cosγ x-τ3 cosτ x α3+β3=γ3+τ3.
α3+β3=γ3+τ3.
α+β=γ+τ,α3+β3=γ3+τ3 α2-αβ+β2=γ2-γτ+τ2,
α2+2αβ+β2=γ2+2γτ+τ2
α2-αβ+β2=γ2-γτ+τ2,
α2+2αβ+β2=γ2+2γτ+τ2
 αβ=γτ, α+β=γ+τ
αβ=γτ, α+β=γ+τ пары(α,β)и(γ,τ)совпадают, что и требовалось.
пары(α,β)и(γ,τ)совпадают, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет