Олимпиадная задача по математике: сумма двух квадратов и оценка разности для n > 10000
Задача
Докажите, что для любого натурального числа n > 10000 найдётся такое натуральное число m, представимое в виде суммы двух квадратов, что
0 < m – n < 3 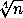 .
.
Решение
Пусть x – наибольшее целое число, квадрат которого не превосходит n: x² ≤ n < (x + 1)². Так как n – целое, n – x² ≤ 2x ≤ 2 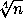 .
.
Пусть y – наименьшее натуральное число, квадрат которого больше n – x²: (y – 1)² ≤ n – x² < y². Тогда
y = (y – 1) + 1 ≤ 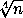 + 1 ≤
+ 1 ≤ 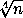 + 1 =
+ 1 = 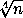
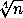 + 1. Ясно, что m = x² + y² > n. С другой стороны,
m – n = x² + y² – n = y² – (n – x²) ≤ y² – (y – 1)² = 2y – 1 ≤ 2
+ 1. Ясно, что m = x² + y² > n. С другой стороны,
m – n = x² + y² – n = y² – (n – x²) ≤ y² – (y – 1)² = 2y – 1 ≤ 2 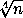
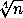 + 1. Осталось заметить, что 0 < 2
+ 1. Осталось заметить, что 0 < 2 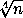
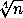 + 1 < 3
+ 1 < 3 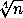 при n > 10000.
при n > 10000.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет