Олимпиадная задача по математике: числитель суммы гармонического ряда, 9

Задача

Докажите, что существует бесконечно много натуральных n, для которых числитель несократимой дроби, равной 1 + ½ + ... + ¹/_n, не является степенью простого числа с натуральным показателем.

Решение

Положим 1 + ½ + ... + ¹/_n = S(n) = ^A(n)/_B(n), где A(n) и B(n) взаимно просты. Заметим, что B(n) > ⁿ/₂. Действительно, наибольшая степень двойки, не превосходящая n, является делителем ровно одного из чисел 1, 2, ..., n и потому является делителем знаменателя суммы S(n).

Предположим, что при всех n ≥ n₀ число A(n) является степенью простого. Пусть p > n₀ + 5 – простое число. Тогда A(p – 1) делится на p (слагаемые суммы S(p – 1) разбиваются на пары, для каждой из которых числитель суммы делится на p). Следовательно, A(p – 1) = p^k. Докажем, по индукции, что числитель A(pⁿ – 1) также кратен p (и, стало быть, является степенью p) при всех натуральных n. База уже доказана.

Шаг индукции. 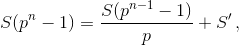где 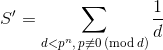(первое слагаемое как раз равно сумме слагаемых со знаменателями, кратными p). Сумма S' разбивается на p^n–1 сумм вида 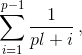l = 0, 1, ..., p^n–1 – 1. Каждая из них имеет числитель, кратный p, что устанавливается как и для S(p – 1). Осталось убедиться, что числитель дроби 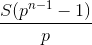делится на p. Действительно, A(p^n–1 – 1) = p^s в силу индуктивного предположения, причём s > 1 (поскольку B(p^n–1 – 1) ≥ ½ p^n–1 ≥ ^p/₂, а S(p^n–1 – 1) ≥ S(n₀ + 4) ≥ S(4) > 2). Положим 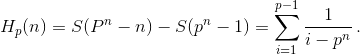Если n > k, то числитель дроби H_p(n) делится на p^k, но не на p^k+1 (ибо H_p(n) – S(p – 1) – дробь, числитель которой делится на pⁿ). Отсюда получаем, что оба числителя A(pⁿ – 1) и A(pⁿ – p) делятся на p, но один из них не делится на p^k+1. Значит, одна из дробей S(pⁿ – 1) и S(pⁿ – p) не превосходит 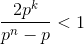при n = k + 2. Противоречие.