Олимпиадная задача по планиметрии и стереометрии для 10–11 класса: сфера и тетраэдр от Емельянова Л. А.
Задача
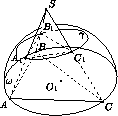
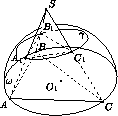
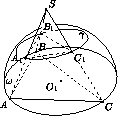
Сфера с центром в плоскости основания ABC тетраэдра SABC проходит через вершины A , B и C и вторично пересекает ребра SA , SB и SC в точках A1, B1и C1соответственно. Плоскости, касающиеся сферы в точках A1, B1и C1, пересекаются в точке O . Докажите, что O – центр сферы, описанной около тетраэдра SA1B1C1.
Решение
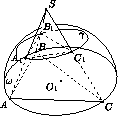
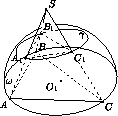
Рис. 1
 1=
1= 2и
2и  2=π-
2=π- A1K1K=
A1K1K= 3,
следовательно
3,
следовательно  1=
1= 3и, значит, AK|| l . Поэтому если β – плоскость, касающаяся σ1в точке S , то AK||β . Поэтому
лучи, проведенные из точки S и пересекающие окружность γ , вторично
пересекают сферу σ в точках, лежащих в одной плоскости τ .
Точки A , B и C лежат в этой плоскости, следовательно τ проходит через
точку O1– центр сферы σ .
3и, значит, AK|| l . Поэтому если β – плоскость, касающаяся σ1в точке S , то AK||β . Поэтому
лучи, проведенные из точки S и пересекающие окружность γ , вторично
пересекают сферу σ в точках, лежащих в одной плоскости τ .
Точки A , B и C лежат в этой плоскости, следовательно τ проходит через
точку O1– центр сферы σ .
 SP1P=
SP1P= SQ1Q=90o,
SQ1Q=90o,
 PQ . Но OP1и OQ1– касательные к окружности с центром O1, поэтому
PQ . Но OP1и OQ1– касательные к окружности с центром O1, поэтому
 SPP1=
SPP1= SQQ1=
SQQ1= OQ1P1=
OQ1P1= OP1Q,
OP1Q,
 Q1OP1=180o-2·
Q1OP1=180o-2· OQ1P1=
2(90o-
OQ1P1=
2(90o- SPP1)=
2·
SPP1)=
2· Q1SP1. Отсюда и из равенства OP1=OQ1следует, что O – центр окружности, описанной около Δ SP1Q1.
Но тогда OS=OP1=OA1=OB1=OC1, т.е. O – центр сферы σ1.
Q1SP1. Отсюда и из равенства OP1=OQ1следует, что O – центр окружности, описанной около Δ SP1Q1.
Но тогда OS=OP1=OA1=OB1=OC1, т.е. O – центр сферы σ1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет