Олимпиадная задача по планиметрии и комбинаторной геометрии для 9–11 классов от В. Л. Дольникова
Задача
На плоскости даны два таких конечных набора P1 и P2 выпуклых многоугольников, что любые два многоугольника из разных наборов имеют общую точку и в каждом из двух наборов P1 и P2 есть пара непересекающихся многоугольников. Докажите, что существует прямая, пересекающая все многоугольники обоих наборов.
Решение
Для каждой из прямых, пересекающих все многоугольники набора P1 , проведем
параллельную ей прямую через центр O некоторой окружности S .
Обозначим через S1множество точек пересечения этих прямых с S .
Определим аналогично для набора P2 множество S2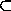 S .
S .
Покажем, что S1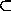 S2=S . Спроектируем многоугольники наборов P1 и P2 на
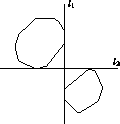
произвольную прямую l (см. рис. 1) . Из условия следует, что при этом получатся два набора отрезков P1' и P2' таких, что любые два отрезка из разных наборов имеют общую точку.
S2=S . Спроектируем многоугольники наборов P1 и P2 на
произвольную прямую l (см. рис. 1) . Из условия следует, что при этом получатся два набора отрезков P1' и P2' таких, что любые два отрезка из разных наборов имеют общую точку.
Возьмем отрезок I , левый конец A которого является среди полученных отрезков самым правым.
Пусть, например, I принадлежит P1' , тогда все отрезки P2' содержат точку A .
Следовательно, прямая m ,
проходящая через точку A перпендикулярно l , пересекает все
многоугольники набора P2.
В силу произвольности выбора прямой l получаем, что S1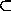 S2=S .
S2=S .
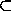
Но если все отрезки из P1' имеют общую точку и все отрезки из P2' имеют общую точку,
то любые два отрезка из P1'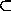 P2' имеют общую точку.
Тогда все отрезки из P1'
P2' имеют общую точку.
Тогда все отрезки из P1'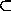 P2' имеют общую точку.
P2' имеют общую точку.
Следовательно, прямая, проходящая через эту точку перпендикулярно l ,
пересекает все многоугольники наборов P1 и P2 .
Таким образом, утверждение задачи доказано,
если S1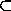 S2
S2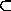
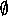 .
.
Покажем, что S1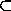 S2
S2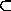
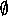 . В самом деле, легко видеть, что
множества S1 и S2 состоят из конечного числа замкнутых
дуг окружности (например, если число элементов в P1 не больше n , то дуг
не больше2Cn2 , так как конец каждой дуги соответствует непересекающимся
многоугольникам; см. рис. 2). Так как в каждом множестве есть пара непересекающихся
многоугольников, то, отделяя эти многоугольники прямой, мы видим, что S1
. В самом деле, легко видеть, что
множества S1 и S2 состоят из конечного числа замкнутых
дуг окружности (например, если число элементов в P1 не больше n , то дуг
не больше2Cn2 , так как конец каждой дуги соответствует непересекающимся
многоугольникам; см. рис. 2). Так как в каждом множестве есть пара непересекающихся
многоугольников, то, отделяя эти многоугольники прямой, мы видим, что S1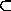 S и S2
S и S2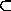 S .
S .
Если S1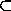 S2=
S2=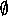 , то S1
, то S1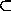 S2 состоит из попарно непересекающихся замкнутых дуг.
Возьмем конец одной
дуги, тогда между ним и ближайшим концом дуги по часовой стрелке нет точек S1
S2 состоит из попарно непересекающихся замкнутых дуг.
Возьмем конец одной
дуги, тогда между ним и ближайшим концом дуги по часовой стрелке нет точек S1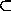 S2 , что противоречит тому, что S1
S2 , что противоречит тому, что S1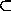 S2=S .
S2=S .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь