Олимпиадная задача по математике на последовательности для 8–10 классов от Голованова А. С.
Задача
Найдите сумму
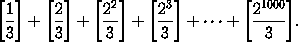
Решение
Уберем первое слагаемое – оно равно 0 – и вместо суммы остальных 1000 слагаемых рассмотрим сумму
Поэтому при замене каждых двух последовательных членов нашей геометрической прогрессии целыми частями сумма уменьшается на 1, а так как в сумме всего 1000 слагаемых, то при замене целыми частями их всех она уменьшится на 500.
Ответ
(21001-2)/3-500.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет