Олимпиадная задача по математике от Дольникова В. Л.: неотрицательные последовательности и геометрические методы
Задача
Дана последовательность неотрицательных чисел a1 , a2 , an . Для любого k от 1 до n обозначим через mk величину
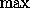 l=1,2,..,k
l=1,2,..,k 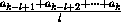 .
.
Решение
 i
i j
j n обозначим через[i,j]отрезок
натурального ряда от i до j . Пусть
n обозначим через[i,j]отрезок
натурального ряда от i до j . Пусть
Выделим в отрезке[1,n]несколько отрезков[pi, qi]по следующему принципу: i -й отрезок начинается с минимального числа p такого, что ap превосходит α и не лежит в ранее построенных отрезках (если такого нет, то построение закончено); заканчивается он таким максимальным q , что при любом j из[pi, q]среднее чисел от api до aj превосходит α . По построению pi+1>qi+1.
Назовем натуральное число k хорошим} если mk>α .
Докажем, что все хорошие числа лежат в построенных отрезках.
Предположим
противное и рассмотрим минимальное хорошее k , для которого
это не так.
Поскольку mk>α , то найдется l k , для которого S(l,k)>α . Так как любое число вне построенных отрезков не
превосходит α , то отрезок[l , k]пересекается с каким-то
отрезком[pj,qj].
k , для которого S(l,k)>α . Так как любое число вне построенных отрезков не
превосходит α , то отрезок[l , k]пересекается с каким-то
отрезком[pj,qj].
Пусть[pi, qi]– самый правый отрезок, лежащий
левее k . Если k>qi+1, то S(qi+2,k) α , откуда S(l,qi+1)>α , что противоречит выбору k .
Поэтому k=qi+1.
Из принципа выбора отрезков следует, что l
α , откуда S(l,qi+1)>α , что противоречит выбору k .
Поэтому k=qi+1.
Из принципа выбора отрезков следует, что l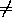 pi (иначе получаем
противоречие с выбором qi ). Если l>pi , то S(pi, l-1)>α ,
откуда S(pi, qi+1)>α , чего не может быть. Если же li , то из S(pi,qi+1)
pi (иначе получаем
противоречие с выбором qi ). Если l>pi , то S(pi, l-1)>α ,
откуда S(pi, qi+1)>α , чего не может быть. Если же li , то из S(pi,qi+1) α следует S(l,pi-1)>α , т.е. pi-1–
хорошее число, не принадлежащее ни одному из отрезков[pj,qj]и
меньшее k , что противоречит сделанному предположению.
α следует S(l,pi-1)>α , т.е. pi-1–
хорошее число, не принадлежащее ни одному из отрезков[pj,qj]и
меньшее k , что противоречит сделанному предположению.
Таким образом, все хорошие k лежат в построенных отрезках.
Получается, что количество хороших чисел не превосходит  (qi-pi+1).
Учитывая, что по построению отрезков [pi,qi]
(qi-pi+1).
Учитывая, что по построению отрезков [pi,qi]
 ak
ak 
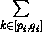 ak>α·
ak>α· (qi-pi+1),
(qi-pi+1),
 b2
b2 ..
.. bn . Тогда
bn . Тогда
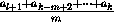 =
=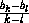 .
.
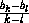 будет равно тангенсу угла
наклона прямой BlBk . Значит, условие mk>α будет равносильно
тому, что прямая, проходящая через Bk с углом наклона arctg,
α (эту прямую назовем lk ) будет проходить выше хотя бы одной из
точек Bl при l<k (такую точку Bk будем называть хорошей). Выражение
будет равно тангенсу угла
наклона прямой BlBk . Значит, условие mk>α будет равносильно
тому, что прямая, проходящая через Bk с углом наклона arctg,
α (эту прямую назовем lk ) будет проходить выше хотя бы одной из
точек Bl при l<k (такую точку Bk будем называть хорошей). Выражение 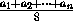 будет равно bn/α , и
это будет расстояние между точкой(n,0)и точкой пересечения ln с
осью абсцисс.
будет равно bn/α , и
это будет расстояние между точкой(n,0)и точкой пересечения ln с
осью абсцисс.
Докажем индукцией по количеству точек n , что это расстояние
больше числа хороших точек.
База очевидна. Если точка Bn не
хорошая, то выбросим ее, при этом число хороших точек не изменится, а отрезок
уменьшится (так как bn-1 bn ). Если же она хорошая, то пусть Bk – ближайшая (по оси абсцисс) точка, лежащая под ln . Тогда выбросим
все точки от Bk+1до Bn (они все хорошие), количество хороших точек
уменьшится на n-k , а отрезок – больше, чем на n-k .
bn ). Если же она хорошая, то пусть Bk – ближайшая (по оси абсцисс) точка, лежащая под ln . Тогда выбросим
все точки от Bk+1до Bn (они все хорошие), количество хороших точек
уменьшится на n-k , а отрезок – больше, чем на n-k .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь