Олимпиадная задача: неравенство для функции одной переменной, авторы Агаханов и Подлипский
Задача
Найдите все функции f :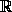 
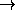
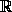, которые для всех x,y,z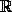
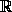удовлетворяют
неравенству
f(x+y)+f(y+z)+f(z+x)
3f(x+2y+3z).
Решение
Положив x=y=-z , получаем f(2x)+f(0)+f(0) 3f(0), откуда f(2x) f(0).
С другой стороны, положив x=z=-y , получаем f(0)+f(0)+f(2x) 3f(2x), откуда f(2x)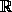
f(0).
Итак, f(0) f(2x) f(0), т.е. f(2x)==C .
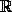
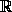Легко проверить, что при любом C функция f(x)= C удовлетворяет
неравенству.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет