Олимпиадная задача по теории чисел для 7-9 классов от Изместьева И. В.
Задача
На доске написаны два различных натуральных числа a и b. Меньшее из них стирают, и вместо него пишут число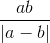 
(которое может уже оказаться нецелым). С полученной парой чисел делают ту же операцию и т.д. Докажите, что в некоторый момент на доске окажутся два равных натуральных числа.
Решение
Одновременно с операциями на доске будем вести запись в тетради. Но вместо каждого числа x, появляющегося на доске, будем писать в тетради число ab/x (a и b – исходные числа). Когда на доске пара чисел (x, y), где x > y, заменяется на пару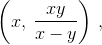 
в тетради происходит замена 
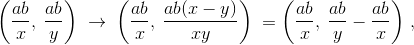то есть, как в алгоритме Евклида, большее число заменяется на разность. Следовательно, на каком-то шаге мы запишем в тетрадь пару чисел, равных (a, b). В это же время оба числа на доске станут равными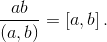 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь