Олимпиадная задача по планиметрии для 7-9 классов: перпендикулярность прямых в треугольнике ABC
Задача
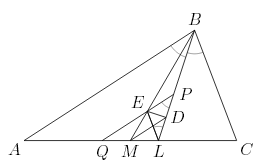
В треугольнике ABC (AB > BC) проведены медиана BM и биссектриса BL. Прямая, проходящая через точку M параллельно AB, пересекает BL в точке D, а прямая, проходящая через L параллельно BC, пересекает BM в точке E. Докажите, что прямые ED и BL перпендикулярны.
Решение
Проведём через точку E прямую, параллельную AB. Пусть она пересекает BL и AC в точках P и Q соответственно. По теореме Фалеса
MO : MA = ME : MB = ML : MC, поэтому MQ = ML. Следовательно, MD – средняя линия треугольника PLQ, то есть ED – медиана треугольника PEL. Из параллельности EP и EL сторонам AB и BC соответственно следует равенство углов: ∠EPL = ∠ABL = ∠LBC = ∠ELP. Тем самым, треугольник LEP – равнобедренный, и медиана ED является высотой.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь