Олимпиадная задача: минимизация времени перевода пяти часов – текстовая задача (7-9 класс)
Задача
На столе лежат пять часов со стрелками. Разрешается любые несколько из них перевести вперёд. Для каждых часов время, на которое при этом их перевели, назовём временем перевода. Требуется все часы установить так, чтобы они показывали одинаковое время. За какое наименьшее суммарное время перевода это можно гарантированно сделать?
Решение
Отметим на одном циферблате положения часовых стрелок всех часов. Циферблат разобьётся на пять секторов. Занумеруем их по кругу (см. рис.).
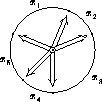
Ответ
За 24 часа.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет