Олимпиадная задача по планиметрии для 10-11 классов — граничные и внутренние окружности выпуклого n-угольника
Задача
Дан выпуклый n -угольник ( n>3), никакие четыре вершины которого не лежат на одной окружности. Окружность, проходящую через три вершины многоугольника и содержащую внутри себя остальные его вершины, назовем описанной. Описанную окружность назовем граничной, если она проходит через три последовательные (соседние) вершины многоугольника; описанную окружность назовем внутренней, если она проходит через три вершины, никакие две из которых не являются соседними вершинами многоугольника. Докажите, что граничных описанных окружностей на две больше, чем внутренних.
Решение
Будем говорить, что три вершины n -угольника ( n>3), через которые проходит описанная окружность, образуют отмеченный треугольник. Докажем, что все отмеченные треугольники образуют триангуляцию многоугольника, т.е. разбиение многоугольника непересекающимися диагоналями на треугольники. Это следует из следующих свойств1)и2)отмеченных треугольников. 1)Никакие два отмеченных треугольника не имеют общей внутренней точки. Действительно, если A1B1C1 и A2B2C2 – различные отмеченные треугольники, а S1 и S2 – сооответствующие описанные окружности, то точки A1 , B1 , C1 расположены на дуге окружности S1 , лежащей внутри S2 , а точки A2 , B2 , C2 – на дуге окружности S2 , лежащей внутри S1 (см. рис.), и утверждение очевидно. Рассуждения не меняются, если одна или две вершины наших треугольников совпадают.
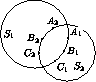
Γ +Π+ B=n-2. (2)
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь