Олимпиадная задача по математике: равенство чисел 19 и 98 за одинаковое число действий

Допустим, что можно, и рассмотрим способ добиться этого за наименьшее количество действий. Пусть a_k , b_k – числа, получавшиеся из 19 и 98 после k -го действия, s – число действий. Тогда a_s=b_s=m и a_s-1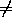 b_s-1(так как мы рассматриваем оптимальный способ).

Действия, проведенные над a_s-1и b_s-1, различны. Значит, m=n² и на(s-1)-м шаге мы имели числа a_s-1=n и b_s-1=n²-1(или наоборот; на дальнейшее решение это не влияет). Общее количество s действий не больше, чем n-18, так как на s-1шаге мы получили n , а каждый шаг увеличивает числа по крайней мере на 1. Тогда n²-1могло получиться только последовательным прибавлением единиц, так как от ближайшего квадрата(n-1)² до n²-1будет2n-2единицы. Следовательно, b₁>(n-1)² , поэтому все числа b₁,..,b_s-1не являются полными квадратами. Поэтому b_s 100, с другой стороны a_s=a_s-1² 19² . Противоречие.

Нельзя.