Олимпиадная задача по планиметрии для 9–11 классов от Шарыгина И. Ф.: особые точки касания вписанной окружности

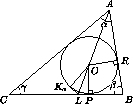
1.Докажем, что стороны треугольника K_aK_bK_c параллельны соответствующим сторонам треугольника ABC . Пусть AC>AB . Имеем POL= K_aOL и POB= ROB (см. рис. 1) , поэтому K_aOR=2 LOB . Угол LOB внешний в треугольнике AOB , значит K_aOR=2(α /2+β /2)=α +β . Случай AC<AB разбирается аналогично. Подобными же рассуждениями получаем, что K_bOR=α +β . Следовательно, точки K_a и K_b симметричны относительно прямой OR , поэтому прямые K_aK_b и AB параллельны. 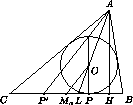Итак, соответствующие стороны треугольников M_aM_bM_c и K_aK_bK_c параллельны ( M_a , M_b , M_c – середины сторон треугольника), поэтому эти треугольники гомотетичны. Центр этой гомотетии является общей точкой прямых M_aK_a , M_bK_b и M_cK_c .

        Рис. 1                               Рис. 2 2.Пусть прямая M_aK_a вторично пересекает вписанную в треугольник ABC окружность в точке T . Будем считать, что AC>AB . Докажем, что описанная вокруг треугольника TK_aL окружность проходит через основание H высоты треугольника ABC . Для этого достаточно проверить выполнение равенства M_aL· M_aH=M_aP² , так как M_aP²=M_aK_a· M_aT (см. рис. 2) . Это можно сделать, выразив длины отрезков M_aP , M_aL и M_aH через стороны треугольника ABC . Мы докажем его, пользуясь известными свойствами точки P' касания со стороной BC соответствующей вневписанной окружности треугольника: точка P' симметрична P относительно M_a и отрезок AP' пересекает вписанную окружность в точке, диаметрально противоположной точке P . Поэтому прямые AP' и M_aO параллельны ( O – центр вписанной окружности, см. рис. 3).         Рис. 3                               Рис. 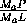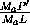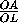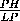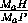4 Пользуясь параллельностью прямых AH и OP , равенством M_aP'=M_aP и теоремой Фалеса, получаем === == , что и требовалось. Так как четырехугольник TK_aLH вписанный, углы M_aTH и M_aLK_a равны. 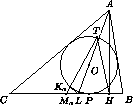Угол M_aLK_a легко выражается через углы треугольника ABC : M_aLK_a=180^o -2 ALB=β -γ (см. рис.) . Рассмотрим теперь четырехугольник M_bTHM_a . Заметим, что HCA= CHM_b=γ (треугольник CM_bH – равнобедренный ), CM_aM_b=β . Поэтому M_aM_bH=β -γ , значит M_aTHM_b – вписанный ( M_aTH= M_aM_bH ) и, следовательно, M_aTM_b=M_aHM_b=γ . 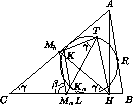Обозначим через K точку пересечения отрезка TM_b со вписанной окружностью. Так как вписанный в окружность угол K_aTK равен γ , а дуга RK_a вписанной окружности равна α +β (это было доказано ранее), точки K_a и K симметричны относительно прямой OR . Но точки K_a и K_b , как отмечено ранее, также симметричны относительно этой прямой. Значит точки K и K_b совпадают, что означает, что прямые M_aK_a и M_bK_b пересекаются в точке T вписанной окружности. Из доказанного следует известная теорема Фейербаха.

Ответ задачи отсутствует