Олимпиадная задача по планиметрии: расстояния между выпуклыми многоугольниками
Задача
Даны два выпуклых многоугольника. Известно, что расстояние между
любыми двумя вершинами первого не больше1, расстояние между
любыми двумя вершинами второго также не больше 1, а расстояние между любыми двумя вершинами разных многоугольников больше,
чем1/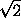
. Докажите, что многоугольники не имеют общих внутренних точек.
Решение
Обозначим через F1 и F2 данные многоугольники. Предположим, что они имеют общую внутреннюю точку. Возможны два случая.
1)Один многоугольник содержится внутри другого, скажем, F1 лежит внутри F2 . Пусть A – одна из вершин F1 . Тогда, как легко видеть,
найдутся три вершины P , Q , R многоугольника F2 такие, что
треугольник PQR содержит A (случай, когда A лежит на стороне
треугольника PQR , легко приводит к противоречию). При этом хотя бы один из
углов PAQ , QAR , RAP больше90o . Пусть, для определенности, 
PAQ
o . Тогда имеем:1 PQ2 AP2+AQ2 .
Получаем, что, вопреки условию, один из отрезков AP и AQ не больше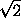 
– противоречие.
2)Сторона одного многоугольника пересекает сторону другого. Пусть,
например, сторона AB многоугольника F1 пересекает сторону PQ многоугольника F2 . Пусть APBQ – выпуклый четырехугольник
(случай, когда среди точек A , B , P , Q найдутся три,
лежащие на одной прямой, легко рассматривается). Хотя бы
один из его углов, скажем, PAQ , не меньше90o .
Тогда1 PQ2 AP2+AQ2 , следовательно, один из
отрезков AP и AQ не больше .
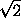Получаем противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь