Олимпиадная задача по комбинаторной геометрии и многочленам для 10-11 класса от Канель-Белова

  Пусть Ф₁, ..., Ф_k– все возможные расположения фигуры Ф в прямоугольнике. Утверждение задачи можно переформулировать так: можно взять фигуры Ф_iтакой неотрицательной толщиныd_i (i= 1, ...,k,  d_iрационально), что суммарная толщина всех фигур Ф_iнад каждой клеткой прямоугольника будет равна 1.   Предположим, что это утверждение неверно.   Введём обозначения: индексом  j (j= 1, ...,mn)  будем нумеровать клетки прямоугольника, индексом  i (i= 1, ...,L)  – положения фигуры Ф на прямоугольнике. Положим  P_ij= 1,  если  j-я клетка закрыта фигурой Ф_i,  P_ij= 0,  если не закрыта. Тогда набору чисел {d_i} соответствует набор чисел 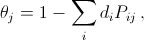   характеризующих уклонение покрытия прямоугольника фигурами от равномерного. По предположению  θ_j≠ 0.   Выберем числа  d_i≥ 0  так, чтобы величина уклонения 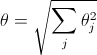   была минимальна (ниже мы докажем, что такой набор существует).   Заменим одно числоd_iна  D_i=d_i + x,  x ≥ – d_i.  Тогда  η_j= θ_j – xP_ij, следовательно, 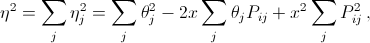  то есть  η² =y(x) =ax² – 2b_ix + c.  Здесь  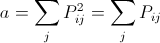  – число клеток в фигуре Ф,  c= θ².  По выбору набора {d_i} квадратный трехчленy(x), заданный на множестве  x ≥ – d_i,  принимает наименьшее значение при  x= 0.  При  d_i> 0  это значит, что  b_i= 0,  а при d_i= 0  – что  b_i≤ 0.  Итак, 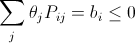   при любомi.   Поставим число θ_jв  j-ю клетку прямоугольника. При этом сумма 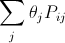   чисел, закрываемых фигурой Ф_i, неположительна, а сумма  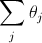  всех чисел в прямоугольнике положительна, так как она равна  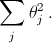  Действительно,  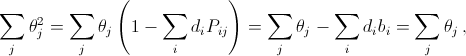  так как  b_i= 0  при  d_i> 0.  Это противоречит условию.   Докажем теперь, что величину θ можно минимизировать.

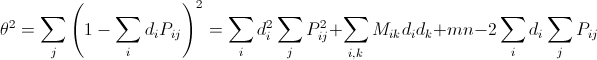
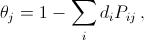
где  M_ik ≥ 0,  а a – число клеток в фигуре Ф. Отсюда следует, что, если  d_i > 2  для некоторого i, то  θ² ≥ a((d_i – 1)² – 1) + mn > mn,  в то время как  θ² = mn,  если все  d_i = 0.  Итак, достаточно рассмотреть функцию θ² на множестве  0 ≤ d₁, ..., d_mn ≤ 2,  то есть на mn-мерном кубе. Непрерывная функция достигает своего наименьшего значения на кубе. Так как это многочлен второй степени с целыми коэффициенты, то координаты этой точки минимума – решение линейной системы уравнений с целыми коэффициентами, то есть рациональны.

Ответ задачи отсутствует