Олимпиадная задача по теории графов для классов 9–11: закрытие 200 городов в стране N

  Рассмотрим граф, вершинами которого являются города, рёбрами – авиалинии. Получится связный граф, степени вершин которого равны 3.

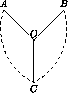
  Предположим, что в этом графе есть два пересекающихся (по вершине) цикла (см. рис.). Рассмотрим вершину O, в которой они разветвляются. Эта вершина, очевидно, имеет степень 3. Удалим её и три выходящих из неё ребра OA, OB, OC. При этом граф сохранит связность, так как существует путь, соединяющий вершины A, B и C.

  Рассмотрим полученный граф. Если в нём есть два пересекающихся цикла, то повторим операцию. И так далее. Заметим, что никакие две удалённые вершины не соединены ребром в исходном графе, так как мы удаляли только вершины степени 3, а после каждой операции степени вершин, соседних с удалённой, уменьшались, то есть они не могут стать равными 3.   Лемма. В связном графе с n вершинами и не менее чем  ⁴ⁿ/₃  рёбрами есть два пересекающихся цикла.

  Доказательство. Предположим, что это не так. В силу связности графа, в нём можно выделить дерево с n вершинами. Будем возвращать в граф оставшиеся после выделения дерева ребра. Добавление каждого ребра увеличивает количество циклов по крайней мере на один. Однако, если какое-либо ребро добавит не менее двух циклов, они будут пересекающимися, что противоречит нашему предположению. С другой стороны, каждый цикл содержит не менее трёх вершин, и никакая вершина не входит в два цикла. Кроме того, дерево с n вершинами содержит ровно  n – 1  ребро. Следовательно, рёбер не более, чем  (n – 1) + ⁿ/₃ < ⁴ⁿ/₃.  Противоречие.   Пусть  N = 1998  – количество вершин в исходном графе, тогда исходное количество рёбер равно ^3N/₂. За каждую операцию выкидывания вершины количество вершин уменьшается на одну, а количество рёбер – на три. Предположим, что было сделано x операций. Тогда стало  N – x  вершин и  ^3N/₂ – 3x  рёбер. До тех пор, пока выполняется неравенство  ^3N/₂ – 3x ≥ ⁴/₃ (N – x)  вершины удалять можно. Решив это неравенство, получаем  x ≤ ^N/₁₀, то есть можно удалить  [¹⁹⁹⁸/₁₀] + 1 = 200  вершин, что и требовалось.

Ответ задачи отсутствует