Олимпиадная задача по планиметрии для 9–11 классов: точки и прямые в треугольнике
Задача
Окружность, вписанная в треугольник ABC, касается сторон BC, CA, AB в точках A1, B1, C1 соответственно. Точки A2, B2, C2 – середины дуг BAC, CBA, ACB описанной окружности треугольника ABC. Докажите, что прямые A1A2, B1B2 и C1C2 пересекаются в одной точке.
Решение
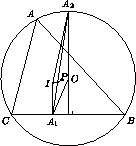
Решение 1: Случай правильного треугольника ABC очевиден. Пусть AB ≠ AC (см. рис.).
Обозначим через O, I центры описанной и вписанной окружностей. Тогда IA1 ⊥ BC и OA2 ⊥ BC. Следовательно, OA2 || IA1 и OA2IA1 – трапеция.
Точка P пересечения диагоналей этой трапеции делит OI в отношении OP : PI = OA2 : IA1 = R : r, где R, r – радиусы соответственно описанной и вписанной окружностей. Проведя аналогичные рассуждения для трапеций OB2IB1, OC2IC1 (если треугольник ABC – равнобедренный, то одна из них вырождается в отрезок) получаем, что отрезки A1A2, B1B2, C1C2 делят OI в отношении R : r и проходят через одну точку P.
Решение 2: Касательная lA в точке A2 к описанной окружности параллельна BC. Рассмотрев касательные lB, lC в точках B2, C2, аналогично получим: lB || AC, lC || AB. Поэтому треугольник ABC гомотетичен треугольнику, образованному прямыми lA, lB, lC. При этой гомотетии A1 переходит в A2, B1 – в B2, C1 – в C2. Следовательно, прямые A1A2, B1B2, C1C2 пересекутся в центре гомотетии.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь