Олимпиадная задача по математике: Вписанная сфера и правильный тетраэдр (10–11 класс)

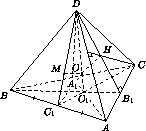
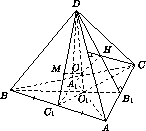
Решение 1:   Пусть O – центр сферы, O₁ – точка пересечения биссектрис треугольника ABC, H – ортоцентр треугольника ACD, M – точка пересечения медиан треугольника ABD и O₁, H, M – точки касания (см. рис.).

  ТочкаO₁– центр вписанной окружности треугольникаABC. Пусть эта окружность касается сторонBC, CAиABв точкахA₁,B₁,C₁соответственно. Тогда  O₁A₁=O₁B₁=O₁C₁,  следовательно, прямоугольные треугольникиOO₁A₁,OO₁B₁,OO₁C₁равны, откуда  ∠OA₁O₁= ∠OB₁O₁= ∠OC₁O₁= φ.  Кроме того,  O₁A₁⊥BC,  поэтому по теореме о трёх перпендикулярах,  OA₁⊥BC,  то есть φ – линейный угол двугранного угла с гранямиBOCиBO₁C. С другой стороны,BOC– биссектор двугранного угла с гранямиBDCиBAC(O– центр вписанной сферы), поэтому угол между гранямиBDCиABCравен 2φ.   Аналогично граниADCиADBнаклонены к основаниюABCпод углом 2φ. Отсюда следует, что проекцияO'точкиDна плоскостьABCравноудалена отAB, BCиCA. Учитывая то, что точкиO'иCлежат по одну сторону отAB, O'иB– отAC, O'иA– отBC, получаем, что  O' = O₁,  то естьDO₁– высота тетраэдра.   Поскольку  AB⊥O₁C₁  и  AB⊥DO₁, то  AB⊥DO₁C₁.   Опустим из точкиOперпендикулярыOH₁иOM₁наDB₁иDC₁. Тогда  OH₁⊥ADC,  так как  OH₁⊥DB₁  и  OH₁⊥AC  (AC⊥DO₁B₁).  Значит,  H₁=H,  то есть  H∈DB₁.   Аналогично,  OM₁⊥ADB,  то есть  M₁=M,  и, значит,  M∈DC₁. Итак, прямаяDM– одновременно медиана и высота треугольникаADB, значит, AD = DB.  Тогда  AO₁=BO₁,  следовательно,  AC = BC  и точки  C, O₁,C₁лежат на одной прямой.   По теореме о трёх перпендикулярах  CO⊥AD  (OH⊥ADC  и  CH⊥AD),  кроме того,  CO AB  (AB⊥CDC₁),  поэтому  CO⊥ADB.  Но  OM⊥ADB,  значит, точкаOлежит наCM. Отсюда следует, чтоM– центр вписанной окружности треугольникаADB(основание конуса с вершинойC, описанного около сферы, – вписанная окружность треугольникаADB, поскольку  CO⊥ADB).    Рассмотрим треугольникCDC₁. В нёмDO₁иCM– высоты,  C₁O– биссектриса, значит,  C₁D = C₁C,  откуда  C₁O₁:O₁C = C₁M:MD= 1 : 2.  Центры вписанных окружностей треугольниковABCиADBявляются точками пересечения медиан, поэтому треугольникиABCиADB– равносторонние.   Отсюда, учитывая то, что высота пирамиды попадает в центр основанияABC, получаем, что тетраэдр – правильный.

Решение 2:   Сделаем развёртку тетраэдра ABCD (см. рис.).

  Пусть сфера касается граниABCв точкеO– центре вписанной окружности, граниACD(треугольникACD₁на рисунке) – в точкеMпересечения медиан, граниBCD(треугольникBCD₂) – в точкеHпересечения высот. По свойству касательных, проведённых к сфере из одной точки,  AM = AO,  CM = CO,  поэтому треугольникиAMCиAOCс общей сторонойACравны. Отсюда  ∠MAC= ∠OAC  и  ∠MCA= ∠OCA.  Из аналогичных равенств для других пар углов получаем, что если  ∠OAC= ∠OAB= α,  ∠OBA= ∠OBC= β  и  ∠OCB= ∠OCA= γ,  то  CAM= α,  ∠CBH= β,  ∠ACM= ∠BCH= γ.  Из треугольникаABC 2α + 2β + 2γ = 180°,  то есть  α + β + γ = 90°,  а из треугольникаBKC: β + γ + ∠HCK= 90°,  значит,  ∠HCK= α.   Отсюда ∠KBD₂= α,  ∠HD₂C= β,  ∠HD₂B= γ  (углы с перпендикулярными сторонами), и  MCD₁= ∠HCD₂= α,  ∠MD₁C= ∠HD₂C= β.  Теперь из треугольникаD₁PC:  ∠D₁PC= 180° – (α + β + γ) = 90°,  значит, медианаD₁Pявляется и высотой треугольникаAD₁C. Отсюда  AD₁=D₁C  и  α = γ (∠MAC= ∠MCA).   Следовательно, треугольникиAD₁TиCD₁Sравны, и значит,  ∠D₁AT= ∠D₁CS= α;  кроме того,D₁P– биссектриса углаAD₁C.   Таким образом, медианаATявляется и биссектрисой треугольникаD₁AC, то есть  ∠AD₁C= ∠ACD₁,  2β = γ + α = 2α.   Итак,  α = β = γ = 60°.  Отсюда следует, что граниABC, ACDиBCDтетраэдра – правильные треугольники, то есть  AB = BC = CA = AD = DC = BD,  значит, тетраэдр – правильный.

Ответ задачи отсутствует