Олимпиадная задача по планиметрии: точки касания окружностей и прямых (8-9 класс)
Задача
Окружности S1 и S2 касаются внешним образом в точке F . Прямая l касается S1 и S2 в точках A и B соответственно. Прямая, параллельная прямой l , касается S2 в точке C и пересекает S1 в двух точках. Докажите, что точки A , F и C лежат на одной прямой.
Решение
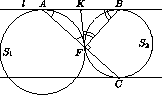
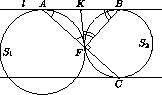 BFC=90o . Докажем, что и
BFC=90o . Докажем, что и  AFB=90o . Проведем через точку F общую
касательную к окружностям (рис),
пусть она пересекает прямую l в точке K . Из равенства отрезков касательных, проведенных к
окружности из одной точки, следует, что треугольники AKF и BKF равнобедренные. Следовательно,
AFB=90o . Проведем через точку F общую
касательную к окружностям (рис),
пусть она пересекает прямую l в точке K . Из равенства отрезков касательных, проведенных к
окружности из одной точки, следует, что треугольники AKF и BKF равнобедренные. Следовательно,
 AFB=
AFB= AFK+
AFK+ KFB=
KFB= FAB+
FAB+ FBA=
FBA=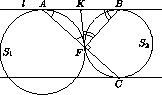 =90o.
=90o.
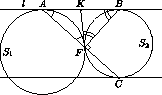 , где r1 и r2 – радиусы окружностей S1 и S2 . При этой гомотетии S1 переходит в S2 , а прямая l –
касательная к S1 – переходит в параллельную прямую – касательную к S2 .
Следовательно, точка A переходит в точку C , поэтому точка F лежит на
отрезке AC .
, где r1 и r2 – радиусы окружностей S1 и S2 . При этой гомотетии S1 переходит в S2 , а прямая l –
касательная к S1 – переходит в параллельную прямую – касательную к S2 .
Следовательно, точка A переходит в точку C , поэтому точка F лежит на
отрезке AC .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет