Олимпиадная задача: Доказательство неравенства пар функций f(x) и g(x) (алгебра, 9–11 класс)
Задача
Функции f(x) и g(x) определены на множестве целых чисел, не превосходящих по модулю 1000. Обозначим через m число пар (x, y), для которых
f(x) = g(y), через n – число пар, для которых f(x) = f(y), а через k – число пар, для которых g(x) = g(y). Докажите, что 2m ≤ n + k.
Решение
Пусть a – одно из значений, принимаемых функцией f(x), а na и ka – количество тех
x, для которых f(x) = a и g(x) = a соответственно (возможно, что ka = 0). Тогда naka пар чисел (x, y) будут удовлетворять равенствам f(x) = g(y) = a, 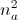 пар – равенствам f(x) = f(y) = a и
пар – равенствам f(x) = f(y) = a и
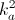 пар – равенствам
пар – равенствам
g(x) = g(y) = a. Поэтому, если a, b, ..., u – все значения, принимаемые функцией f, то
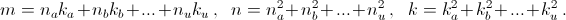
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь