Олимпиадная задача по математике: доказательство о делимости дробей для 7-9 класса
Задача
Даны такие натуральные числаaиb, что число a+1/b+b+1/a является целым.
Докажите, что наибольший общий делитель чиселaиbне превосходит числа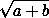 
.
Решение
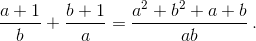Пусть d = НОД(a, b). Так как ab делится на d², то a² + b² + a + b делится на d². Число a² + b² также делится на d². Поэтому a + b делится на d² и 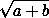≥ d.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет