Олимпиадная задача по планиметрии для 7–9 классов от Вавилова В.: равные сечения прямоугольных треугольников
Задача
Три прямоугольных треугольника расположены в одной полуплоскости относительно данной прямой l так, что один из катетов каждого треугольника лежит на этой прямой. Известно, что существует прямая, параллельная l, пересекающая треугольники по равным отрезкам. Докажите, что если расположить треугольники в одной полуплоскости относительно прямой l так, чтобы другие их катеты лежали на прямой l, то также найдётся прямая, параллельная l , пересекающая их по равным отрезкам.
Решение
На рисунке слева отрезки, отмеченные двумя штрихами, равны по условию, а отрезки отмеченные одним штрихом, также равны, так как l1 || l.
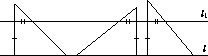
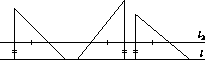
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет